Perbandingan Trigonometri

 

Trogonometri adalah cabang matematika yang mempelajari hubungan antara sisi dengan sudut dalam sebuah segitiga. Trigonometri telah dikembangkan sejak abad 3 SM dan menjadi dasar bagi pengembangan ilmu astronomi, teknik sipil, arsitektur, permesinan, dan lain-lain. 

Contoh penerapan lain trigonometri adalah dalam bidang militer, menentukan sudut serang untuk peluncur senjata agar proyektil tepat sasaran. Menentukan kemiringan jalan di daerah pegunungan agar aman dilalui kendaraan juga menerapkan trigonometri. Dalam pembangunan jembatan, trigonometri digunakan dalam penentuan titik simpul jembatan. Menentukan jarak kapal dari dermaga, ketinggian pohon, menghitung ketegangan tali yang diberi beban, dan banyak aplikasi lainnya.

Mari pelajari perbandingan trigonometri agar mendapat manfaat dan ilmu yang menarik!

Definisi Perbandingan Trigonometri

Perbandingan trigonometri didefinisikan sebagai perbandingan sisi-sisi dalam sebuah segitiga siku-siku. Perbandingan trigonometri terdiri dari sinus ⟮sin⟯, cosinus ⟮cos⟯, dan tangen ⟮tan⟯. 

Misalkan sebuah segitiga siku-siku ABC dengan siku-siku di titik C, seperti gambar berikut.

Maka perbandingan sinus, cosinus, dan tangen untuk sudut A pada segitiga ABC di atas adalah sebagai berikut.

Sinus A: 

$\boxed {\sin A=\frac{a}{c}}$

Cosinus A: 

$\boxed {\cos A=\frac{b}{c}}$

Tangen A: 

$\boxed {\tan A=\frac{a}{b}}$

Perbandingan sinus, cosinus, dan tangen untuk sudut B pada segitiga ABC di atas adalah sebagai berikut.

Sinus B: 

$\boxed {\sin B=\frac{b}{c}}$

Cosinus B: 

$\boxed {\cos B=\frac{a}{c}}$

Tangen B: 

$\boxed {\tan B=\frac{b}{a}}$

 

Contoh Soal.

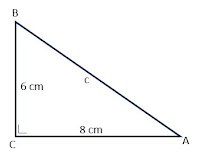
Sebuah segitiga siku-siku yang siku-siku di titik C, memiliki panjang sisi-sisi siku-siku 6 cm dan 8 cm. Hitunglah sin A, cos A, tan A, sin B, cos B, dan tan B!

Jawab.

Berikut ini sketsa segitiga ABC.

Perhitungan sisi c :

\begin{array}{rcl} c^{2}&=&a^{2}+b^{2} \\ c^{2}&=&6^{2}+8^{2}\\ c^{2}&=&36+64 \\ c^{2}&=&100\\ c&=&\sqrt{100}\\ c&=&10 \end{array}  

Sinus A: 

$\sin A=\frac{a}{c}=\frac{6}{10}=0,6$

Cosinus A: 

$\cos A=\frac{b}{c}=\frac{...}{...}=...$

Tangen A: 

$\tan A=\frac{a}{b}=\frac{...}{...}=...$

Sinus B: 

$\sin B=\frac{b}{c}=\frac{...}{...}=...$

Cosinus B: 

$\cos B=\frac{a}{c}=\frac{...}{...}=...$

Tangen B: 

$\tan B=\frac{b}{a}=\frac{...}{...}=...$

Latihan

1. Sebuah segitiga siku-siku yang siku-siku di titik B, memiliki panjang sisi-sisi siku-siku AB = 15 cm dan BC = 8 cm. Hitunglah sin A, sin C, dan tan A.
2. Segitiga ABC siku siku di titik B, dengan panjang sisi miring 25 cm, dan sin A = 0,96. Berapakah nilai Tan A?
   

Share :